Cryptology and Security systems - Caesar & Vigenère
2 - First algorithms and their implementation in Java, C, C++
- 2.1 Caesar Cipher
2.1.1 The shift cipher
2.1.2 Application example
2.1.3 Breaking the Caesar cipher
2.1.4 Is it adviced to use this cipher?
2.1.5 Programming Caesar cipher in Java and C
2.1.6 Appendix: Histogram frequency of the french, german, spanish and english letters
2.1.7 Exercices
- 2.2 Vigenere Cipher
2.2.1 Introduction and Encryption Principle
2.2.2 The Table of Vigenère
2.2.3 Encryption
2.2.4 Mathematical principle of encryption and decryption
2.2.5 Vigenere Cipher (and method of Kasiski and Friedman) programmed with C
2.2.6 Exercices
2.1 Caesar Cipher
2.1.1 The shift cipher
The shift cipher, also called Caesar encryption, is simply a decaler of the alphabet letters either to the right or to the left.
To encode a text you just have to replace each letter of your message with the letter of the alphabet at a fixed distance. If we decide to make a lag of three to the right as did Julius Caesar the letter "A" will be replaced by "D", B by E, C F, ... as shown in the following shema:
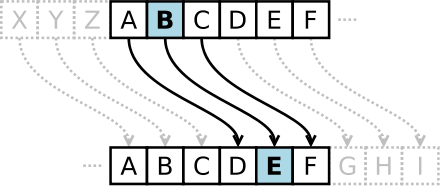
The (private) key for encryption is "right shift 3" without which the recipient cannot decode the message to read it.
2.1.2 Application example
| Plaintext | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| After encoding | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C |
Make the test yourself, you can even make the online encryption or decryption (do not use accents):
2.1.3 Breaking the Caesar cipher
There are several methods to break this code:- Research by the method of encryption:
The cryptanalyst notice a lag of regularity with shifts and deduce that the Caesar code has been used.. - Research by the offset also called attack by the brute force:
The cryptanalyst does not know the number of offset and will tests all the possibilities which in fact are not really big .. - By frequency analysis:
The cryptanalyst analysis the frequency of occurrence letter and creates an array of frequency then he compares it to the letters of the used language..
(Method Used: Search the offset)
2.1.4 Is it adviced to use this cipher?
This encryption system is just an alphabet decaler and as we only have 25 letters so there are only 25 possible keys, so it is so easy to break encryption as we so in the application test. We can in the worst case test all opportunities.2.1.5 Programming Caesar cipher with Java and C
With Java
public class Caesar {
public static final char[] alpha =
{'A','B','C','D','E','F','G','H','I','J','K','L','M',
'N','O','P','Q','R','S','T','U','V','W','X','Y','Z'};
protected char[] texte_code = new char[26];
protected char[] texte_clair = new char[26];
public Caesar(Integer decalage) {
for (int i=0; i < 26; i++) texte_code[i] = alpha[(i + decalage) % 26];
for (int i=0; i < 26; i++) texte_clair[texte_code[i] - 'A'] = alpha[i]; }
public String codage(String secret) {
char[] message = secret.toCharArray();
for (int i=0; i < message.length; i++)
if (Character.isUpperCase(message[i]))
message[i] = texte_code[message[i] - 'A'];
return new String(message);
}
public String decodage(String secret) {
char[] message = secret.toCharArray();
for (int i=0; i < message.length; i++)
if (Character.isUpperCase(message[i]))
message[i] = texte_clair[message[i] - 'A'];
return new String(message);
}
public static void main(String[] args) {
Caesar message = new Caesar();
System.out.println("Alphabet 1 = " + new String(message.texte_code));
System.out.println("Alphabet 2 = " + new String(message.texte_clair));
String secret = "CAIUS JULIUS CAESAR";
secret = message.texte_code(secret); System.out.println(secret);
secret = message.texte_clair(secret); System.out.println(secret);
}
}
With C
#include
#include
void cesar_encode(int decalage, const char *texte_clair, char *texte_code);
void cesar_decode(int decalage, const char *texte_code, char *texte_clair);
int main(int argc, char *argv[]){
char *texte_clair = "Ave, Caesar, morituri te salutant !";
char *texte_code = malloc(strlen(texte_clair)+1);
char *resultat = malloc(strlen(texte_clair)+1);
cesar_encode(10, texte_clair,texte_code);
cesar_decode(10, texte_code,resultat);
printf("-->original : %s\n-->texte code : %s\n-->texte clair : %s\n",
texte_clair, texte_code, resultat);
free(texte_code); free(resultat); system("PAUSE"); return 0;
}
void cesar_encode(int decalage, const char *texte_clair, char *texte_code){
int i, length = strlen(texte_clair);
for(i = 0; i < length; i++){
if (!isalpha(texte_clair[i])){ texte_code[i] = texte_clair[i]; }
else{
texte_code[i] = (tolower(texte_clair[i]) + decalage - 'a')& + 'a';
}
} texte_code[i] = '\0';
}
void cesar_decode(int decalage, const char *texte_code, char *texte_clair){
int i, length = strlen(texte_code);
for(i = 0; i < length; i++){
if (!isalpha(texte_code[i])){
texte_clair[i] = texte_code[i];
}
else{
texte_clair[i] = (tolower(texte_code[i]) - 'a' - decalage + 26)& + 'a';
}
}
texte_clair[i] = '\0';
}
2.1.6 Appendix: Histogram frequency of the french, german, spanish and english letters
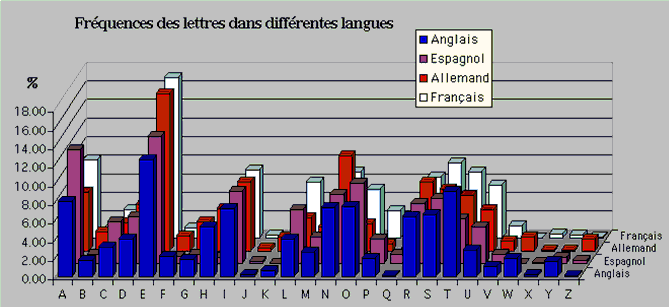
2.1.7 Exercices
EncodingEncrypt, using a paper, the following message with the Caesar cipher shifting letters 7 places to the left:
bachosdesign is the best website.
I learn many things on it.
Vérifiez votre cryptogramme avec le programme ci-dessus.
Decoding
Decipher, using a paper, the text below encrypted with the Caesar Cipher by shifting the letters of 6 places to the left OR to the right, you have to try and to know:
HGINU YJKYO MTKYZ RKSKO RRKAX YOZKJ GVVXK TZOYY GMK
(To check your answer user the program of this page)
2.2 Vigenère Cipher
2.2.1 Introduction and Principle of encryption
The Vigenere Cipher is a polyalphabetic encryption system and a substitution cipher, but a single letter of the plaintext may, depending on its position in it, can be replaced by different letters, which is not the case for the system of encryption monoalphabetic of Caesar Cipher (though he uses as a component). This method thus resistant to frequency analysis, which is a decisive advantage over monoalphabétiques ciphers. However the number of Vigenere was broken by the Prussian Major Friedrich Kasiski who published his method in 1863.
It introduces the concept of encryption key. A key is usually in the form of a word or phrase. To quantify our text, for each character we use a letter key to perform the substitution. Obviously, more the key is long and varied better text will be encrypted. You should know that there was a period where entire passages of literary works were used to encrypt the biggest secrets. Both parties had only to have in their hands a copy of the same book to ensure proper understanding of the messages.
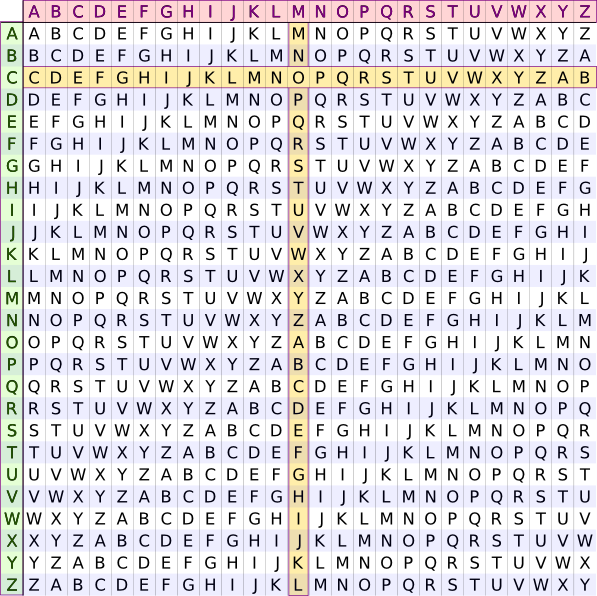
2.2.2 Table of Vigenère
The essential tool of Vigenère encryption is "Vigenère table" which will be very useful for following the course
Table of Vigenère.
Lettre en clair A B C D E F G H I J K L M N O P Q R S T U V W X Y Z C
l
é
U
t
i
l
i
s
é
e
A A B C D E F G H I J K L M N O P Q R S T U V W X Y Z L
e
t
t
r
e
c
h
i
f
f
r
é
e
B B C D E F G H I J K L M N O P Q R S T U V W X Y Z A C C D E F G H I J K L M N O P Q R S T U V W X Y Z A B D D E F G H I J K L M N O P Q R S T U V W X Y Z A B C E E F G H I J K L M N O P Q R S T U V W X Y Z A B C D F F G H I J K L M N O P Q R S T U V W X Y Z A B C D E G G H I J K L M N O P Q R S T U V W X Y Z A B C D E F H H I J K L M N O P Q R S T U V W X Y Z A B C D E F G I I J K L M N O P Q R S T U V W X Y Z A B C D E F G H J J K L M N O P Q R S T U V W X Y Z A B C D E F G H I K K L M N O P Q R S T U V W X Y Z A B C D E F G H I J L L M N O P Q R S T U V W X Y Z A B C D E F G H I J K M M N O P Q R S T U V W X Y Z A B C D E F G H I J K L N N O P Q R S T U V W X Y Z A B C D E F G H I J K L M O O P Q R S T U V W X Y Z A B C D E F G H I J K L M N P P Q R S T U V W X Y Z A B C D E F G H I J K L M N O Q Q R S T U V W X Y Z A B C D E F G H I J K L M N O P R R S T U V W X Y Z A B C D E F G H I J K L M N O P Q S S T U V W X Y Z A B C D E F G H I J K L M N O P Q R T T U V W X Y Z A B C D E F G H I J K L M N O P Q R S U U V W X Y Z A B C D E F G H I J K L M N O P Q R S T V V W X Y Z A B C D E F G H I J K L M N O P Q R S T U W W X Y Z A B C D E F G H I J K L M N O P Q R S T U V X X Y Z A B C D E F G H I J K L M N O P Q R S T U V W Y Y Z A B C D E F G H I J K L M N O P Q R S T U V W X Z Z A B C D E F G H I J K L M N O P Q R S T U V W X Y
2.2.3 Vigenere encryption
To encode a message, we choose a key which can be a word of arbitrary length. This key is then written in the message to be encoded by repeating it as often as necessary to keep always a letter of the key under each letter of the message to be encoded. To encode, we look in the table of the intersection line of the letter code with the column letter of the key.
Exemple : On veut coder le texte "CRYPTOGRAPHIE DE VIGENERE" avec la clé "MATHWEB". On commence par écrire la clef sous le texte à coder :
Table of Vigenère.
| Lettre en clair | ||||||||||||||||||||||||||||
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | |||
C | A | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | L |
| B | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | ||
| C | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | ||
| D | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | ||
| E | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | ||
| F | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | ||
| G | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | ||
| H | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | ||
| I | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | ||
| J | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | ||
| K | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | ||
| L | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | ||
| M | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | ||
| N | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | ||
| O | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | ||
| P | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | ||
| Q | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | ||
| R | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | ||
| S | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | ||
| T | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | ||
| U | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | ||
| V | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | ||
| W | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | ||
| X | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | ||
| Y | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | ||
| Z | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | ||
| C | R | Y | P | T | O | G | R | A | P | H | I | E | D | E | V | I | G | E | N | E | R | E |
| M | A | T | H | W | E | B | M | A | T | H | W | E | B | M | A | T | H | W | E | B | M | A |
We find O. Then we continue. We find : ORRWPSHDAIOEI EQ VBNARFDE. This encryption algorithm has many strengths. It is very easy to use, and decryption is just as easy if you know the key. Just on the column letter of the key, to find the letter of the coded message. At the left end of the line, there is the letter of the plaintext. You can train with the coded message TYQFLJ, we coded the EKETHR key. In addition, the above example show the great feature of Vigenere code: the letter E was coded I, A, Q, and E. Impossible by a simple statistical analysis to find where the E. Last thing, we can produce an infinite number of keys and it is very easy to agree with someone of a particular key. He resisted the work of cryptanalysts until the nineteenth century. Yet, with few exceptions, such as in the correspondence of Marie-Antoinette, the figure and the figures more generally poly-alpha, were little used. They are preferred codes directories.
Here is a program that allow you to encode and decode a message, online to better understand the system. Enter an unaccented message.
2.2.4 Mathematical principle of encryption and decryption
Encryption principle
The encryption uses a key composed of letters, to encrypt, you take the first letter of the message and the first letter of the key is added (letters have a value of A = 0 to Z = 25, the sum modulo 26 is taken), and we note the letter of the result. If the length of the key is smaller than the text length, returns to the beginning of the key.
More you choose a long key, more the code is difficult to decipher.
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
Plaintext : BACHOS DESIGN EST LE TOP SITE Repeated key : KEYKEY KEYKE YKE YK EYK YKEY The first letter value is: B + K = 1+10 = 11 mod 26 = 11 which means L. Doing the same thing on all the letters of the message we obtain the ciphertext : LEARSQ NIQSKL OWR VI RYT QSXC
Decryption principle
Decryption is the reverse of the encryption method, all what you have to do is to subtract the key to the message.
Ciphertext : LEARSQ NIQSKL OWR VI RYT QSXC Repeated key : KEYKEY KEYKE YKE YK EYK YKEY The first letter value is : L - K = 11 - 10 = 1 mod 26 = 1 soit B. Plaintext : BACHOS DESIGN EST LE TOP SITE
Cryptanalysis (without key)
We can notice that all the letters spaced k (where k is the length of the key) are offset in the same constant.
So just make a frequency analysis for each sub-texts. The challenge is to find the length of the key, without it, you can not decrypt.
Méthode de Indice de coincidence
L'indice de coïncidence représente la probabilité que deux lettres choisies aléatoirement dans un texte soient identiques. Pour la langue française, l'IC est environ égal à 0.074, cet indice ne varie pas si le texte est codé avec une substitution monoalphabétique. En testant différentes longueur de clé, et en conservant les longueurs pour lesquelles l'IC est le plus proche de 0.074, on peut en déduire la longueur de la clé.
Method and test of Kasiski
Kasiski method is to look for repetitions in the ciphertext. Usually we look for at least 3 letters repetition. The idea is that the same sequence of letters of the plaintext was encrypted with the same part of the key and then the same sequence of letters was repeated in the ciphertext. Noting that using the number of letters that separate redundant sequences we can obtain a multiple of the length of the key.
Repetitiona separated by 24 characters and another separated by 16 characters pattern are identified. We look for common factors, the key can be of length 1, 2, 4 or 8.
Principle of Brute-Force
Based on the idea of SingeMalicieux research the program search the likely lengths most key and then calculates the possible keys to simplify the analysisef from frequency looking for the letter E.
2.2.5 Vigenere Cipher and method of Kasiski and Friedman C
Method of Kasiski
maths.h
-------
#ifndef MATH_HEADER
#define MATH_HEADER
long int gcd(long int a, long int b);
float fabs_p(float f);
int round_p(float f);
#endif
maths.c
-------
#include "math.h"
// PGCD par l'algorithme d'Euclide
long int gcd(long int a, long int b)
{
long int c;
if (a < b){c = a;a = b;b = c;}
while (b != 0){c = a % b;a = b;b = c;}
return a;
}
float fabs_p(float f)
{
if (f < 0){return -f;
} else {return f;}
}
int round_p(float f)
{
int i;
i = (int) f;
if (f - (float) i >= .5f){i++;}
return i;
}
kasiski.h
----------
#ifndef KASISKI_HEADER
#define KASISKI_HEADER
float CalcFreqDist(float freq1[26], float freq2[26], int shift);
int FindBestShift(float ref_freq[26], float freq[26]);
#endif
kasiski.c
----------
#include "kasiski.h"
#include "math.h"
// Calcule la 'distance' entre 2 analyses fréquentielles en ayant décalé la première de vers la droite
float CalcFreqDist(float freq1[26], float freq2[26], int shift)
{
float dist = 0;
int i;
for (i = 0; i < 26; i++)
{
dist += fabs_p(freq1[i] - freq2[(i+shift)%26]);
}
return dist;
}
// Renvoie le décalage sur la première analyse fréquentielle minimisant la distance.
int FindBestShift(float ref_freq[26], float freq[26])
{
int shift = 0,i;
float dist, min_dist = CalcFreqDist(ref_freq, freq, 0);
for (i = 1; i < 26; i++)
{
dist = CalcFreqDist(ref_freq, freq, i);
if (dist < min_dist)
{
min_dist = dist;
shift = i;
}
}
return shift;
}
Friedman method
lang.h
---------
#ifndef LANG_HEADER
#define LANG_HEADER
typedef struct {
float coincidence;
float freq[26];
char id[3];
} lang_t;
lang_t LoadLang(char *file_name);
#endif
lang.c
---------
#include "lang.h"
#include
#include
lang_t LoadLang(char *lang_code)
{
FILE *file;
char *file_name, *content;
int file_size, i = 0;
lang_t lang;
lang.id[0] = lang_code[0];
lang.id[1] = lang_code[1];
lang.id[2] = 0;
while (lang_code[i] > 0) i++;
file_name = malloc(i+4+1);
sprintf(file_name, "%s.dat", lang_code);
if (( file = fopen(file_name, "r") ) == NULL )
{
printf("Erreur lors de l'ouverture du fichier %s\n", file_name);
exit(-1);
}
// On calcule la taille du fichier
fseek(file, 0, SEEK_END);
file_size = ftell(file);
fseek(file, 0, SEEK_SET);
content = malloc(file_size+1);
if (fgets(content, file_size, file) != NULL)
{
sscanf(content, "%f", &(lang.coincidence)); // On récupère l'indice de coincidence
} else {
printf("Erreur: Ficher de langue '%s' incomplet !\n", file_name);
exit(-1);
}
// Puis les fréquences
for (i = 0; i < 26; i++)
{
if (fgets(content, file_size, file) != NULL)
{
sscanf(content, "%f", &(lang.freq[i]));
} else {
printf("Erreur: Ficher de langue '%s' incomplet !\n", file_name);
exit(-1);
}
}
fclose(file);
free(content);
free(file_name);
return lang;
}
text_analyser.h
--------------
// Analyse d'un texte (fréquences, répétitions, indice de corrélation, ...)
#ifndef TEXT_ANALYSER_HEADER
#define TEXT_ANALYSER_HEADER
#include "buffer.h"
typedef struct {
long int cnt[26];
long int size;
float freq[26];
float coincidence;
} text_stats_t;
void GetFrequencies(text_stats_t* text_stats, buffer_t* text, long int step, long int shift);
void GetCoincidence(text_stats_t* text_stats);
// Affiche un comparatif de fréquences
void DrawFrequencies(float freq[26], float ref_freq[26], int height);
#endif
text_analyser.c
--------------
#include "text_analyser.h"
#include "buffer.h"
#include "math.h"
#include
#include
void GetFrequencies(text_stats_t* text_stats, buffer_t* text, long int step, long int shift)
{
unsigned long int i;
if (text->size == 0)
{
printf("Analyse des frequences d'un texte vide impossible !\n");
exit(-1);
}
for (i = 0; i < 26; i++)
{
text_stats->cnt[i] = 0;
}
text_stats->size = 0;
for (i=shift; i < text->size; i += step)
{
text_stats->cnt[(unsigned char)text->content[i]]++;
text_stats->size ++;
}
for (i=0; i < 26; i++)
{
text_stats->freq[i] = (float) text_stats->cnt[i] / (float) text_stats->size;
}
}
void GetCoincidence(text_stats_t* stats)
{
int i;
stats->coincidence = 0;
for (i = 0; i < 26; i++)
{
stats->coincidence += ((float) stats->cnt[i]/stats->size) * ((float) (stats->cnt[i]-1) / (stats->size - 1));
}
}
// Affiche un comparatif de fréquences
void DrawFrequencies(float freq[26], float ref_freq[26], int height)
{
float max = 0;
int heights[26], heights_ref[26];
unsigned char c;
int x, y;
div_t div_result;
// On cherche la fréquence maximum
for (c = 0; c < 26; c++)
{
if (freq[c] > max) max = freq[c];
if (ref_freq[c] > max) max = ref_freq[c];
}
// On calcule la hauteur de chaque 'barre'
for (c = 0; c < 26; c++)
{
heights[c] = round_p(freq[c] / max * (float) height);
heights_ref[c] = round_p(ref_freq[c] / max * (float) height);
}
// Dessin du graphe
for (y = 0; y < height; y++)
{
for (x = 0; x <= 3*26-1; x++)
{
div_result = div(x,3);
if (div_result.rem == 0)
{
if (heights[div_result.quot] >= height - y)
{
printf("#");
} else {
printf(" ");
}
}
else if (div_result.rem == 1 )
{
if (heights_ref[div_result.quot] >= height - y)
{
printf("|");
} else {
printf(" ");
}
}
else printf(" ");
}
printf("\n");
}
// Affichage des lettres
for (x = 0; x <= 3*26-1; x++)
{
div_result = div(x,3);
if (div_result.rem < 2)
{
printf("%c", 65 + div_result.quot);
} else printf(" ");
}
printf("\n");
}
friedman.h
--------------
#ifndef FRIEDMAN_HEADER
#define FRIEDMAN_HEADER
#include "text_analyser.h"
#include "lang.h"
typedef struct {
long int length;
float* coincidence;
text_stats_t* stats;
} friedman_t;
typedef struct {
long int length;
float dist;
} key_length_t;
// Calcule la suite des indices de coincidence du texte en prenant les caractères tous les 'length' caractères
friedman_t* GetFriedman(buffer_t *text, long int length);
// Libère la mémoire
void ReleaseFriedman(friedman_t *friedman);
// Renvoie la 'distance' de la liste de coincidence par rapport à un indice de référence
// Cette 'distance' est en fait la moyenne de la différence de chaque indice avec celui de référence
float CalcFriedmanDist(friedman_t *friedman, float ref_coincidence);
// Renvoie la longueur de clé minimisant la 'distance' à l'indice de référence
key_length_t FindBestKeyLength(buffer_t *text, float ref_coincidence, long int length_max);
// Cherche la langue la plus adaptée et la meilleure longueur de clé correspondante
int FindLangAndKeyLength(buffer_t *text, long int length_max, lang_t *lang_list, int nb_lang, key_length_t *best_key);
// Dessine à l'écran le graphe des distances à l'indice de référence, en fonction de la longueur de la clé
void DrawDistGraph(buffer_t *text, float ref_coincidence, long int length_max, int height);
#endif
friedman.c
--------------
#include "friedman.h"
#include "text_analyser.h"
#include "math.h"
#include
#include
// Calcule la suite des indices de coincidence du texte en prenant les caractères tous les 'length' caractères
friedman_t* GetFriedman(buffer_t *text, long int length)
{
long int i;
friedman_t *friedman = malloc(sizeof(friedman_t));
friedman->coincidence = malloc(length * sizeof(float));
friedman->stats = malloc(length * sizeof(text_stats_t));
friedman->length = length;
for (i = 0; i < length; i++)
{
GetFrequencies(friedman->stats + i, text, length, i);
GetCoincidence(friedman->stats + i);
friedman->coincidence[i] = friedman->stats[i].coincidence;
}
return friedman;
}
// Libère la mémoire
void ReleaseFriedman(friedman_t *friedman)
{
free(friedman->coincidence);
free(friedman->stats);
free(friedman);
}
// Renvoie la 'distance' de la liste de coincidence par rapport à un indice de référence
// Cette 'distance' est en fait la moyenne de la différence de chaque indice avec celui de référence
float CalcFriedmanDist(friedman_t *friedman, float ref_coincidence)
{
long int i;
float dist = 0;
for (i = 0; i < friedman->length; i++)
{
dist += fabs_p(friedman->coincidence[i] - ref_coincidence);
}
return dist / (float) friedman->length;
}
// Renvoie la longueur de clé minimisant la 'distance' à l'indice de référence
key_length_t FindBestKeyLength(buffer_t *text, float ref_coincidence, long int length_max)
{
long int length, best_length = 1;
friedman_t *friedman = GetFriedman(text, best_length);
float dist, min_dist = CalcFriedmanDist(friedman, ref_coincidence);
key_length_t best_key;
ReleaseFriedman(friedman);
for (length = 2; length <= length_max; length++)
{
friedman = GetFriedman(text, length);
dist = CalcFriedmanDist(friedman, ref_coincidence);
ReleaseFriedman(friedman);
if (dist < min_dist)
{
min_dist = dist;
best_length = length;
}
}
best_key.dist = min_dist;
best_key.length = best_length;
return best_key;
}
// Dessine à l'écran le graphe des distances à l'indice de référence, en fonction de la longueur de la clé
void DrawDistGraph(buffer_t *text, float ref_coincidence, long int length_max, int height)
{
float *dist_list, dist, max_dist = 0;
int *height_list;
friedman_t *friedman;
long int length;
int x, y;
dist_list = malloc(length_max * sizeof(float));
// On calcule les indices et on en profite pour récupérer le max
max_dist = 0;
for (length = 1; length <= length_max; length++)
{
friedman = GetFriedman(text, length);
dist = CalcFriedmanDist(friedman, ref_coincidence);
ReleaseFriedman(friedman);
dist_list[length-1] = dist;
if (dist > max_dist) max_dist = dist;
}
// On calcule la hauteur des 'barres' correspondantes
height_list = malloc(length_max * sizeof(int));
for (length = 1; length <= length_max; length++)
{
height_list[length-1] = round_p(dist_list[length-1]/max_dist * (float) height);
}
// Dessin du graphe
for (y = 0; y < height; y++)
{
for (x = 1; x <= length_max; x++)
{
if (height_list[x-1] >= height - y)
{
printf("#");
} else {
printf(" ");
}
}
printf("\n");
}
// Dessin de l'axe des abscisses
for (x = 1; x <= length_max; x++)
{
printf("=");
}
printf("\n");
// Dessin des graduations
for (x = 1; x <= length_max; x++)
{
if (x % 10 == 0)
{
printf("#");
} else if (x % 5 == 0) {
printf("|");
} else {
printf(" ");
}
}
printf("\n");
}
// Cherche la langue la plus adaptée et la meilleure longueur de clé correspondante
int FindLangAndKeyLength(buffer_t *text, long int length_max, lang_t *lang_list, int nb_lang, key_length_t *best_key)
{
int i, best_lang;
key_length_t curr_key;
*best_key = FindBestKeyLength(text, lang_list[0].coincidence, length_max);
best_lang = 0;
for (i = 1; i < nb_lang; i++)
{
curr_key = FindBestKeyLength(text, lang_list[i].coincidence, length_max);
if (curr_key.dist < best_key->dist)
{
*best_key = curr_key;
best_lang = i;
}
}
return best_lang;
}
viginere.c (exemple basique à ameliorer)
--------------
#include stdio.h
#include stdlib.h
#include string.h
#include math.h
void filtrage(char *file_name, char *contenu, char *filtrer);
void cryp_decryp(char *filtrer, char *clef, char *crypt, int s);
void frequence(char *filtrer, char *contenu);
void filtrage1(char *contenu);
int main()
{
char contenu[2001];
char filtrer[2001], clef[2000], crypt[2001];
/* tableau : le 1 est reserv? au 0*/
int nombre[26] = {0};
float ind=0;
char c;
int s;
filtrage("acrypter.txt", contenu, filtrer);
printf("\nLe text sans caracteres speciaux (en minuscules) est:\n");
printf("------------------------------------------------------\n");
printf("%s\n\n", filtrer);
printf("Veuillez Donner la Clef (en minuscules):\n");
printf("----------------------------------------\n");
scanf("%s%*[^\n]", &clef);
getchar();
printf("Tapez (c) pour Crypter et (d) pour decrypter: \n");
printf("---------------------------------------------\n");
c = getchttp://www.google.fr/firefox?client=firefox-a&rls=com.ubuntu:en-US:officialhar();
if (c == 'c')
{
s = 1;
} else if (c == 'd') {
s = -1;
} else {
printf("Mauvais choix, Aurevoir !\n");
exit(-1);
}
cryp_decryp(filtrer, clef, crypt, s);
printf("Le cryp_decryp du text correspondant a cette clef est:\n");
printf("------------------------------------------------------\n");
printf("%s\n\n", crypt);
/*text a decrypter:
indice de coincidence, nombre d'apparition des lettres et leur frequence*/
filtrage1 (contenu);
frequence (filtrer, contenu);
printf("\n\n");
scanf("%*[^\n]");
getchar();
printf("Appuyez sur une touche ...\n");
getchar();
return 0;
}
void frequence(char *filtrer, char *contenu)
{
int nombre[26] = {0},i,j,n,counter, taille;
float ind=0, dist,distance[10]={0.0};
FILE *f_input;
// ouverture du fichier adecrypter ? la lecture
f_input = fopen("adecrypter.txt", "r");
if(f_input==NULL)
{
printf("Error: Impossible d'ouvrir le fichier.\n");
exit(-1);
}
counter = 0;
while (! feof(f_input) && counter < 2000)
{
contenu[counter++] = fgetc(f_input);
}
fclose(f_input); /* pour fermer le fichier */
contenu[counter] = 0; /* pour terminer la chaine*/
i = 0; j = 0;
while(contenu[i])
{
if (contenu[i] >= 'a' && contenu[i] <= 'z')
{
filtrer[j++] = contenu[i]; // caractere minuscule, aucun probleme
}
else if (contenu[i] >= 'A' && contenu[i] <= 'Z')
{
filtrer[j++] = 'a' + ( contenu[i] - 'A' ); /// on transforme en minuscule
}
i++;//on incr?mente la position dans le texte
}
filtrer[j] = 0; // pour terminer la chaine
// on vas essayer de trouver la longuer de la clef:on suppose que la taille de la clef est <= 10
printf("\nLes indices de coincidences:\n");
printf("------------------------------\n");
for (n=1; n <=10; n++)
{
dist = 0.0;
for (j = 0; j < n; j++){
for (i=0; i < 26; i++){
nombre[i] = 0;
}
taille = 0;
for (i=j;i< strlen(filtrer);i+=n)
{
nombre[filtrer[i]-'a']++;
taille++; //taille du message aussi = strlen(filtrer)
}
//Indice de coincidence:
for (i=0;i<26;i++)
ind= ind + nombre[i]*(nombre[i]-1);
ind=ind/(float)(taille*(taille-1));
printf("l'indice de coincidence pour n=%d et j=%d est: %f\n", n, j, ind);
//distance entre les lettres du messages et celles de l'alphabet (sachant que la langue est le francais)
dist += fabs(ind - 0.074);
}
printf("\n\n");
dist = dist / (float) n;
distance[n]=dist;
}
for(i=1;i<=10;i++)
printf("distance[%d]: %f\n",i,distance[i]);
}
/* Cryptage ou Decryptage selon vigenere*/
void cryp_decryp(char *filtrer, char *clef, char *crypt, int s)
{
int i = 0, j = 0;
while (filtrer[i])
{
crypt[i] = (filtrer[i] - 'a' + s*(clef[j] - 'a') + 26)%26 + 'a';
/* Cryptage lettre par lettre par Vigenere */
i++;
if (clef[++j] == 0) /* Repetition de la Clef */
j = 0;
}
crypt[i] = 0; /* pour terminer la chaine afin d'eviter un bug*/
}
2.2.6 Exercices
Encoding
Encrypt, on a paper, the following figure with the Vigenere using the key "bach"
bachos design is here, always to help meCheck your cryptogram with the program above.
Decoding
Decipher, on a paper, the following figure with the Vigenere using the keyword "BACHOS"
DHKMT JFDGC WYFNG YSHBR DHQZP S