Traitement d�images
R�dig� par Mr. Bachir Jean EL HAGE
Universit� Joseph Fourier � INPG
Grenoble 1 - FRANCE
A. Introduction
Dans les �coles, lyc�es et m�me aux seins des �tablissements universitaires on se pose toujours la question suivante :
A quoi servent les maths ?
Tout d�abord les maths nous procurent � un esprit critique � nous permettant de raisonner avec logique et de mieux dialoguer dans notre vie quotidienne, de convaincre et de critiquer un argument.
D�accord mais Mr � part �a ? Un m�decin n�a pas besoin des maths ! Un informaticien non plus !
Bien s�r que si. Les maths sont aussi le c�ur de toutes les recherches scientifiques, de tout le progr�s m�dical et informatique. La physique bien �videment se base sur les maths, l�astronomie aussi, la s�curit� des syst�me et la chiffrement des codes�
Vous avez certainement regard� vos photos sur un ordinateur, vous avez aussi essay� de faire un zoom. Vous avez peut �tre utilis� des logiciels comme adobe Photoshop ou autre pour retoucher vos photos, am�liorer la qualit� d�une image pix�lis�e ou mal scann� ou flout�e.
Vous savez aussi que la police poss�de des logiciels de reconnaissance faciale qui arrive � reconnaitre un visage avec un minimum de donn�es. Grace � une �photo de basse qualit� prise avec une cam�ra de surveillance on arrive quand m�me � reconnaitre la personne en question avec certitude !
Mais �tes-vous demand� un jour comment cela fonctionne-t-il ? Pensiez-vous que tout cela se joue gr�ce aux math�matiques ? Aux polyn�mes, fonctions, d�riv�es premi�re et d�riv�e seconde,� sinus, cosinus, tangentes, � ?
Je vais tenter de vous expliquer dans la suite de ce document comment intervient les math�matiques dans le traitement d�images tout en vous proposant th�orie et exemples r�alis�s sous Matlab pour une compr�hension optimale du sujet propos�.
B. Interpolation et approximation (d�finitions et exemples)
1. G�n�ralit�
En analyse num�rique� l'interpolation est une op�ration math�matique permettant de construire une courbe � partir de la donn�e d'un nombre fini de points, ou une fonction � partir de la donn�e d'un nombre fini de valeurs. La solution du probl�me d'interpolation passe par les points prescrits, et, suivant le type d'interpolation, il lui est demand� de v�rifier des propri�t�s suppl�mentaires.
L�interpolant 
est
g�n�ralement construit de l�unique fonction s��crivant sous la forme :
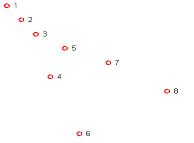
Exemple d�interpolation par Spline :
|
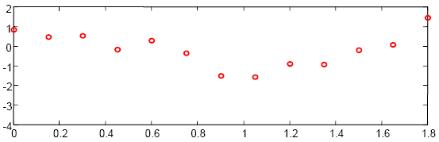
Nombre fini de points distribu� al�atoirement :
|
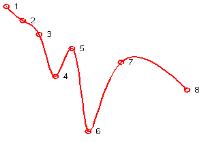
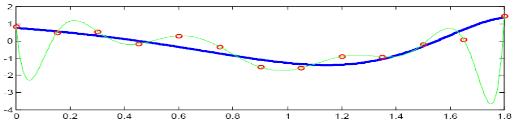
Apr�s interpolation (par Spline) :
|
2. Probl�me
Ayant un nombre fini de points on
cherche � d�terminer une fonction 
�passant par ses points qui soit
facile � �valuer. Le probl�me c�est qu�il existe une infinit� de
solutions !
Ce qu�il faut alors faire c�est de se restreindre � une famille de fonctions : exponentielle, polyn�mes, fonctions trigonom�triques, �
3. Interpolation lin�aire
Le type le plus simple d'interpolation est l'interpolation lin�aire, qui consiste � joindre les points donn�s. Elle peut servir � estimer les valeurs situ�es entre les donn�es de la table.
Par exemple, si nous souhaitons
d�terminer 
�alors
que l'on connait les valeurs de 
, on
prend la moyenne des 2 valeurs sachant que 2,5 est le milieu des 2 points.
On obtient par cons�quent
Plus g�n�ralement, la droite d'interpolation aura pour �quation (trois formulations �quivalentes) :
Ou bien (formule de Taylor-Young au premier ordre) :
Ou bien :
Cette derni�re formule correspond � la moyenne pond�r�e.
|
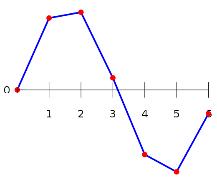
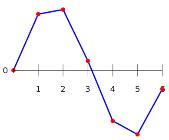
Les points rouges correspondent aux points
( |
Cette m�thode est
rapide et ais�e mais elle manque de pr�cision. Elle pr�sente aussi l�inconv�nient
de ne pas �tre d�rivable au point �
.
L'erreur d'estimation
montre que l'interpolation lin�aire n'est pas tr�s pr�cise. Si la fonction 
�que l'on souhaite
interpoler est deux fois continument d�rivable et si 
�alors l'erreur
d'interpolation est donn�e par :
En d'autres termes, l'erreur est proportionnelle au carr� de la distance entre les n�uds.
D'autres m�thodes d'interpolation permettent d'obtenir des fonctions d'interpolation plus lisses, par exemple, l'interpolation polynomiale
4. Interpolation polynomiale de type Lagrange
Th�or�me
�Soient 
�points distincts 
r�els et �r�els 
, il existe un unique
polyn�me 
�tel que 
�pour 
.
Construction du
polyn�me 
:
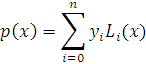
��tant le
polyn�me de Lagrange et est d�finie par :
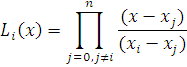
Propri�t� de 
:
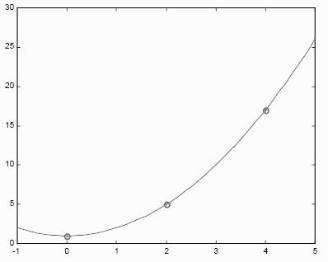
Exemple d�application
Soit � trouver le polyn�me interpolant les 3 points suivants
(0 ; 1) , (2 ; 5) et (4 ; 17)
Les polyn�mes de Lagrange associ�s sont
Calculons alors le polyn�me d�interpolation
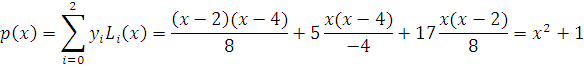
L�algorithme et le r�sultat de l�exemple sous Matlab :
|
Fonction (P)=lagrange(X,Y) n= nombre de points. x=poly(0,"x");P=0; pour i=1 � n, L=1; pour� j=[1:i-1,i+1:n] L=L*(x-X(j))/(X(i)-X(j)); � Fin pour P=P+L*Y(i); Fin pour Fin fonction
Compilation : -->X=[0;2;4]; Y=[1;5;17]; P=lagrange(X,Y) P = 1 + x^2 |
|
L�interpolation polynomiale est facile � comprendre et � programmer, elle donne en plus des bons r�sultats avec une erreur minimale.
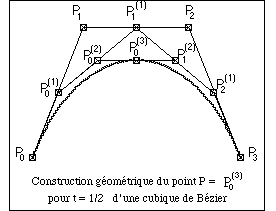
5. Approximation et courbes de B�zier
|
L'interpolation doit �tre distingu�e de l'approximation de fonction, qui consiste � chercher la fonction la plus proche possible, selon certains crit�res, d'une fonction donn�e. Les courbes de B�ziers sont un exemple d�approximation :
|
|
Dans le cas de l'approximation, il n'est en g�n�ral plus impos� de passer exactement par les points donn�s initialement. Ceci permet de mieux prendre en compte le cas des erreurs de mesure, et c'est ainsi que l'exploitation de donn�es exp�rimentales pour la recherche de lois empiriques rel�ve plus souvent de la r�gression lin�aire, ou plus g�n�ralement de la m�thode des moindres carr�s.
Apr�s l�explication th�orique de l�interpolation et de la mani�re dont on trouve le polyn�me ou la fonction ou la courbe interpolant un nombre fini de points, nous allons passer tout de suite � son utilit� dans le traitement d�images !
C. Comment l'interpolation fonctionne-t-elle ?
Dans notre recherche nous nous concentrerons exclusivement sur la fonction de l'interpolation dans le contexte de la r�solution d'image.
L'interpolation est un proc�d� d'estimation de valeur entre deux informations pr�existantes. Il est utilis� dans les scanners, les appareils num�riques et les logiciels d'�dition d'images afin de produire une image avec une r�solution (le nombre de pixels verticaux et horizontaux) plus grande que celle captur�e par le capteur.
Simplement formul�, l'interpolation "invente" des pixels l� o� il n'y en avait pas et les intercale entre deux originaux pour augmenter la taille d'image. Si cela semble �tre de la triche-et c'est parfois effectivement le cas. Les images ci-dessous montrent le m�canisme d'une simple interpolation. Notez que dans une interpolation r�elle des pixels de couleur, ceux-ci serait de couleur identique � celle des originaux environnants.���
|
|
|
|
Il existe diff�rentes m�thodes pour interpoler une image: Lin�aire, Bilin�aire, Bicubique et Fractale. Toutes tentent d'augmenter la taille de l'image tout en limitant au maximum les effets d'un tel processus.
G�n�ralement, le probl�me majeur avec l'interpolation est qu'elle peut augmenter fortement un d�faut de l'image en l'agrandissant. L'interpolation Bicubique est habituellement consid�r�e comme la meilleure m�thode, mais pourtant, il arrive qu'elle ne produise pas les meilleurs r�sultats.
L'interpolation fonctionne le mieux lorsqu'elle est appliqu�e � petite dose et sur une grande quantit� d'informations. Une image constitu�e d'une faible quantit� de pixels montrera plus de trace de d�gradation qu'une image plus riche au d�part. Dans tous les cas, l'interpolation n'inventera pas des d�tails qui ne se trouvaient pas dans l'image originale.�
1. Utilit� de l�interpolation
En terme informatique, l�interpolation est un proc�d� qui permet d'augmenter la r�solution d'une image num�ris�e en d�finissant des pixels interm�diaires entre des pixels r�els gr�ce � un algorithme math�matique, en calculant la moyenne des couleurs des pixels avoisinants. Cette technologie permet donc d'obtenir des r�sultats int�ressants.
Toshiba a d�velopp� une nouvelle technique de super-r�solution pour la cr�ation de haute r�solution d�images ou vid�o � partir de ceux � faible r�solution.
Si une partie de l'image est agrandie, la d�gradation de la qualit� d'image et l'image reste incertain, m�me si l'interpolation est effectu�e en douceur entre les pixels.
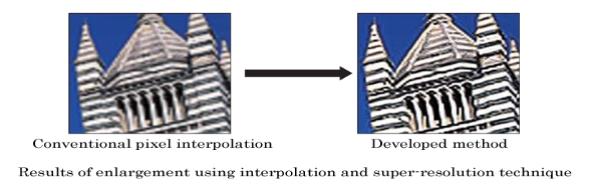
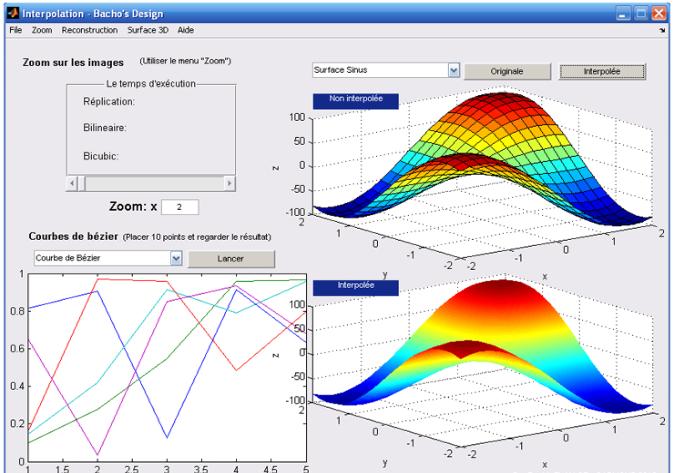
2. Quelques r�sultats int�ressants cr��s sous Matlab :
Avec une bonne connaissance de Matlab on arrive � cr�er son propre logiciel capable de faire un zoom sur les images en gardant une bonne qualit�, de cr�er des surfaces en 3D colori�es en utilisant des fonctions math�matiques telles le sinus, le cosinus ou l�exponentielle. D�utiliser l�interpolation pour fusionner les couleurs, �
|
|
Jeux de cosinus, sinus, etc. :
|
|
|
|
L�interpolation permet aussi de corriger le flou d�une image
En travaillant sur la direction du flou et sur des caract�ristiques de la vitesse on peut utiliser l�espace de Fourier pour avoir le r�sultat suivant :
|
|
|
Etes-vous toujours convaincu que les Maths ne servent � rien ?
D. D�tection des contours
Le but de la d�tection de contours est de rep�rer les points d'une image num�rique qui correspondent � un changement brutal de l'intensit� lumineuse. Ces changements de propri�t�s de l'image traduisent en g�n�ral des �v�nements importants ou des changements dans les propri�t�s du monde. Ils incluent des discontinuit�s dans la profondeur, dans l'orientation d'une surface, dans les propri�t�s d'un mat�riau et dans l'�clairage d'une sc�ne. La d�tection de contour est un champ de la recherche qui appartient au traitement d'image et � la vision par ordinateur, particuli�rement dans le domaine de l'extraction de caract�ristiques.
La d�tection des contours d'une image r�duit de mani�re significative la quantit� de donn�es et �limine les informations qu'on peut juger moins pertinentes, tout en pr�servant les propri�t�s structurelles importantes de l'image. Il existe un grand nombre de m�thodes de d�tection de l'image mais la plupart d'entre elles peuvent �tre regroup�es en deux cat�gories. La premi�re recherche les extremums de la d�riv�e premi�re, en g�n�ral les maximums locaux de l'intensit� du gradient. La seconde recherche les annulations de la d�riv�e seconde, en g�n�ral les annulations du laplacien ou d'une expression diff�rentielle non-lin�aire.
Il existe plusieurs model pour la d�tection des contours :
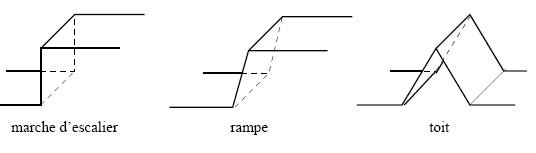
Quelques mod�les de contours. Le plus utilis� est celui en marche d�escalier.
Un contour est caract�ris� par un changement brutal de la valeur. Le but de l'op�ration est de transformer cette image en une autre dans laquelle les contours apparaissent par convention en blanc sur fond noir.
Dans une section horizontale (ou verticale) de l'image rectangulaire, les variations de la valeur sont d�crites par une courbe. Sur celle-ci un point d'un contour est associ� � un maximum de la pente, c'est-�-dire � un extremum (maximum ou minimum) de la d�riv�e premi�re. Cet extremum peut aussi s'interpr�ter comme un z�ro de la d�riv�e seconde.
Dans une image num�ris�e, � chaque pixel est associ�e une valeur qui est en g�n�ral diff�rente de la valeur des pixels voisins. La notion de d�riv�e correspondant � une variation infiniment petite doit donc �tre remplac�e par l'approximation diff�rence finie utilis�e en calcul num�rique. Le probl�me est simplifi� car on ne s'int�resse ici qu'aux comparaisons entre d�riv�es ind�pendamment de leurs valeurs. Ainsi la d�riv�e premi�re au niveau d'un pixel se r�duit � la diff�rence entre les valeurs des deux pixels voisins, la d�riv�e seconde �tant la diff�rence entre les d�riv�es moyenn�es aux fronti�res des pixels.
La d�tection de contour est tr�s utile en traitement d'images, c'est par exemple une �tape indispensable � la reconnaissance de formes. Ces algorithmes sont �galement utilis�s en imagerie m�dicale, cartographies, ...
La d�tection des contours de Marr / Hildreth
La d�tection des contours de Marr / Hildreth est bas�e sur les passages par z�ro du Laplacien de l'op�rateur gaussien appliqu� � l'image pour diff�rentes valeurs de sigma, l'�cart-type de la gaussienne. Ce qui donne une mosa�que de passages � z�ro pour quatre choix de Sigma calcul� en utilisant la bo�te � outils de traitement d'image Matlab.
Exemple d�tection des contours de l�image suivante (programm� avec Matlab):
R�sultat de la d�tection utilisant le Filtre de Canny (� gauche) puis� Marr/Hildreth (� droite)
|
|
|
Haut : � gauche est sigma = 1, �� droite est sigma = 2, Bas :� � gauche est sigma = 3, � droite est sigma = 4.
(Matlab Laplacian of Gaussian la d�tection de contour s�lectionne normalement un seuil, afin que seuls les passages par z�ro de la force suffisante soient affich�s. Ici, le seuil est forc� � z�ro afin que tous les passages par z�ro sont rapport�s, comme c'est requis par th�orie de d�tection de pointe de Marr / Hildreth.)
Nous ne rentrerons pas dans les d�tails des formules math�matiques utilis�es par ces proc�d�s. Nous nous contenterons des r�sultats trouv�s et de leur utilit�.
Domaine d�application
En astrologie par exemple, on d�sire � partir d�un clich� pris par un t�lescope, pouvoir d�tecter de nouveaux corps c�lestes. Par ailleurs, en imagerie m�dicale, il est important de pouvoir d�celer des tumeurs canc�reuses, � partir d�une scanographie. Dans l�exemple qui suit, nous pr�senterons une des nombreuses m�thodes de d�tection utilis�es en reconnaissance faciale et en imagerie satellite.
Des chercheurs allemands ont d�velopp� une nouvelle technologie d'analyse faciale rapide.
Elle permet d'identifier un visage humain sur une photo (ce que Google Images fait d�j�), et est capable de diff�rencier un visage d'homme ou de femme, et d'analyser l'expression du visage (content / triste, etc...).
E. Codage d'une image, repr�sentation spatiale
Une image est consid�r�e comme un ensemble de points ou pixels (picture element), associ�s au quadrillage rectangulaire de l'image d'origine. La repr�sentation d'une image se fait donc par l'interm�diaire d'une matrice d'entiers cod�s entre 0 et 255. Les images en niveau de gris sont repr�sent�es par des matrices 2D, les images couleurs repr�sent�s par 3 composantes (Rouge, Vert, Bleu) sont repr�sent�es par des matrices 3D. On acc�de � un pixel gr�ce a son indice de ligne et son indice de colonne. Le premier pixel d'une image est le pixel en haut � gauche. Cette repr�sentation est appel� repr�sentation spatiale de l'image.
Dans un prochain projet j�expliciterais aussi le domaine de la cryptographie et l�utilit� des math�matique dans les syst�mes bancaire et tous les programmes travaillant sur la s�curit� de l�information.
F. Conclusion
J�esp�re vous avoir donn� ne serait-ce qu�une petite id�e sur l�utilit� des math�matiques. Vous n�avez d�sormais plus le droit de dire � les maths �a ne sert � rien �.
Mettez-vous au travail de la mati�re la plus importante de toutes les mati�res.
R�dig� par Mr. Bachir Jean EL HAGE
Universit� Joseph Fourier � INPG
Grenoble 1 - FRANCE
www.bachosdesign.com